[1]:
import emat
from emat.util.loggers import timing_log
emat.versions()
emat 0.5.2, plotly 4.14.3
Meta-Model Creation¶
To demostrate the creation of a meta-model, we will use the Road Test example model included with TMIP-EMAT. We will first create and run a design of experiments, to have some experimental data to define the meta-model.
[2]:
import emat.examples
scope, db, model = emat.examples.road_test()
design = model.design_experiments(design_name='lhs')
results = model.run_experiments(design)
We can then create a meta-model automatically from these experiments.
[3]:
from emat.model import create_metamodel
with timing_log("create metamodel"):
mm = create_metamodel(scope, results, suppress_converge_warnings=True)
<TIME BEGINS> create metamodel
< TIME ENDS > create metamodel <18.05s>
If you are using the default meta-model regressor, as we are doing here, you can directly access a cross-validation method that uses the experimental data to evaluate the quality of the regression model. The cross_val_scores provides a measure of how well the meta-model predicts the experimental outcomes, similar to an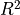 
measure on a linear regression model.
[4]:
with timing_log("crossvalidate metamodel"):
display(mm.cross_val_scores())
<TIME BEGINS> crossvalidate metamodel
| Cross Validation Score | |
|---|---|
| no_build_travel_time | 0.9946 |
| build_travel_time | 0.9846 |
| time_savings | 0.9242 |
| value_of_time_savings | 0.8345 |
| net_benefits | 0.6746 |
| cost_of_capacity_expansion | 0.8952 |
| present_cost_expansion | 0.9445 |
< TIME ENDS > crossvalidate metamodel <14.22s>
We can apply the meta-model directly on a new design of experiments, and use the contrast_experiments visualization tool to review how well the meta-model is replicating the underlying model’s results.
[5]:
design2 = mm.design_experiments(design_name='lhs_meta', n_samples=10_000)
[6]:
with timing_log("apply metamodel"):
results2 = mm.run_experiments(design2)
<TIME BEGINS> apply metamodel
< TIME ENDS > apply metamodel <0.18s>
[7]:
results2.info()
<class 'emat.experiment.experimental_design.ExperimentalDesign'>
Int64Index: 10000 entries, 0 to 9999
Data columns (total 20 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 alpha 10000 non-null float64
1 amortization_period 10000 non-null int64
2 beta 10000 non-null float64
3 debt_type 10000 non-null category
4 expand_capacity 10000 non-null float64
5 input_flow 10000 non-null int64
6 interest_rate 10000 non-null float64
7 interest_rate_lock 10000 non-null bool
8 unit_cost_expansion 10000 non-null float64
9 value_of_time 10000 non-null float64
10 yield_curve 10000 non-null float64
11 free_flow_time 10000 non-null int64
12 initial_capacity 10000 non-null int64
13 no_build_travel_time 10000 non-null float64
14 build_travel_time 10000 non-null float64
15 time_savings 10000 non-null float64
16 value_of_time_savings 10000 non-null float64
17 net_benefits 10000 non-null float64
18 cost_of_capacity_expansion 10000 non-null float64
19 present_cost_expansion 10000 non-null float64
dtypes: bool(1), category(1), float64(14), int64(4)
memory usage: 1.5 MB
[8]:
from emat.analysis import contrast_experiments
contrast_experiments(mm.scope, results2, results)
No Build Time
Build Time
Time Savings
Value Time Save
Net Benefits
Cost of Expand
Present Cost
Design Sizing¶
An important advantage of using a Latin hypercube design of experiments, as is the default in TMIP-EMAT, is that the required number of experimental runs is not directly dependent on the dimensionality of the input variables and, importantly, does not grow exponentially with the number of dimensions. With a factorial or grid-based design, the number of experiments required does expand exponentially with the number of input dimensions.
Practical experience across multiple domains has led to a “rule of thumb” that good results for prediction (i.e., for the creation of a meta-model) can usually be obtained from 10 experimental data points per input variable dimension (Loeppky et al., 2009). This can still lead to a sizable number of experiments that need to be undertaken using a core model, if there are a large number of uncertainties and policy levers to consider. When defining an exploratory scope, which defines the number and definition of uncertainties and policy levers, analysts will want to carefully consider the tradeoffs between the number of experiments to be run, the resources (i.e. runtime) needed for each core model experiment, and the detail needed to adequately describe and model both uncertainties and policy levers in the context of the overall policy goals being considered.
If the underlying core model is generally well behaved, and has reasonable and proportional performance measure responses to changes in input values, then it may be possible to successfully develop a good-fitting meta-model with fewer than 10 experiments per input dimension. Unfortunately, for all but the most basic models it is quite difficult to ascertain a priori whether the core model will in fact be well behaved, and general “rules of thumb” are not available for this situation.
Ultimately, if the dimensionality of the inputs cannot be reduced but a project cannot afford to undertake 10 model experiments per dimension, the best course is to specifically develop a design of experiments sized to the available resource budget. This can be done using the n_samples arguments of the design_experiments function, which allows for creating a design of any particular size. It is preferable to intentionally create this smaller design than to simply run a subset of a larger
Latin Hypercube design, as smaller design will provide better coverage across the uncertainty space.
Whether a design of experiments is sized with 10 experiments per input variable, or fewer, it remains important to conduct a (cross-)validation for all meta-modeled performance measures, to ensure that meta-models are performing well. The 10x approach is a “rule of thumb” and not a guarantee that enough experimental data will be generated to develop a high quality meta-model in any given circumstance. Indeed, the guidance from Loeppky et al. is not simply that 10x is enough, but rather that either (a) 10x will be sufficient or (b) the number of experiments that will actually be sufficient is at least an order of magnitude larger.
Performance measures that are poorly behaved or depend on complex interactions across multiple inputs can give poor results even with a larger number of experiments. For example, in the Road Test meta-model shown above, the “net benefits” performance measure exhibits a heteroskedastic response to “expand amount” and also rare high-value outliers that are dependent on at least 3 different inputs aligning (input flow, value of time, and expand amount). In combination, these conditions make it difficult to properly meta-model this performance measure, at least when using the automatic meta-modeling tools provided by TMIP-EMAT. The low cross-validation score reported for this performance measure reflects this, and serves as a warning to analysts that the meta-model may be unreliable for this performance measure.
Partial Metamodels¶
It may be desirable in some cases to construct a partial metamodel, covering only a subset of the performance measures. This is likely to be particularly desirable if some of the performance measures are poorly fit by the meta-model as noted above, or if a large number of performance measures are included in the scope, but only a few are of particular interest for a given analysis. The time required for generating and using meta-models is linear in the number of performance measures included, so if you have 100 performance measures but you are only presently interested in 5, your meta-model can be created much faster if you only include the 5 performance measures. It will also run much faster, but the run time for metamodels is so small anyhow, it’s likely you won’t notice.
To create a partial meta-model for a curated set of performance measures, you can use the include_measures argument of the create_metamodel command.
[9]:
with timing_log("create limited metamodel"):
mm2 = create_metamodel(
scope, results,
include_measures=['time_savings', 'present_cost_expansion'],
suppress_converge_warnings=True,
)
with timing_log("crossvalidate limited metamodel"):
display(mm2.cross_val_scores())
with timing_log("apply limited metamodel"):
results2_limited = mm2.run_experiments(design2)
results2_limited.info()
<TIME BEGINS> create limited metamodel
< TIME ENDS > create limited metamodel <4.30s>
<TIME BEGINS> crossvalidate limited metamodel
| Cross Validation Score | |
|---|---|
| time_savings | 0.8847 |
| present_cost_expansion | 0.8987 |
< TIME ENDS > crossvalidate limited metamodel <5.17s>
<TIME BEGINS> apply limited metamodel
< TIME ENDS > apply limited metamodel <0.07s>
<class 'emat.experiment.experimental_design.ExperimentalDesign'>
Int64Index: 10000 entries, 0 to 9999
Data columns (total 15 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 alpha 10000 non-null float64
1 amortization_period 10000 non-null int64
2 beta 10000 non-null float64
3 debt_type 10000 non-null category
4 expand_capacity 10000 non-null float64
5 input_flow 10000 non-null int64
6 interest_rate 10000 non-null float64
7 interest_rate_lock 10000 non-null bool
8 unit_cost_expansion 10000 non-null float64
9 value_of_time 10000 non-null float64
10 yield_curve 10000 non-null float64
11 free_flow_time 10000 non-null int64
12 initial_capacity 10000 non-null int64
13 time_savings 10000 non-null float64
14 present_cost_expansion 10000 non-null float64
dtypes: bool(1), category(1), float64(9), int64(4)
memory usage: 1.1 MB
There is also an exclude_measures argument for the create_metamodel command, which will retain all of the scoped performance measures except the enumerated list. This can be handy for dropping a few measures that are not working well, either because the data is bad in some way or if the measure isn’t well fitted using the metamodel.
[10]:
with timing_log("create limited metamodel"):
mm3 = create_metamodel(
scope, results,
exclude_measures=['net_benefits'],
suppress_converge_warnings=True,
)
with timing_log("crossvalidate limited metamodel"):
display(mm3.cross_val_scores())
with timing_log("apply limited metamodel"):
results3_limited = mm3.run_experiments(design2)
results3_limited.info()
<TIME BEGINS> create limited metamodel
< TIME ENDS > create limited metamodel <14.58s>
<TIME BEGINS> crossvalidate limited metamodel
| Cross Validation Score | |
|---|---|
| no_build_travel_time | 0.9917 |
| build_travel_time | 0.9774 |
| time_savings | 0.9113 |
| value_of_time_savings | 0.8366 |
| cost_of_capacity_expansion | 0.9110 |
| present_cost_expansion | 0.9415 |
< TIME ENDS > crossvalidate limited metamodel <12.07s>
<TIME BEGINS> apply limited metamodel
< TIME ENDS > apply limited metamodel <0.14s>
<class 'emat.experiment.experimental_design.ExperimentalDesign'>
Int64Index: 10000 entries, 0 to 9999
Data columns (total 19 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 alpha 10000 non-null float64
1 amortization_period 10000 non-null int64
2 beta 10000 non-null float64
3 debt_type 10000 non-null category
4 expand_capacity 10000 non-null float64
5 input_flow 10000 non-null int64
6 interest_rate 10000 non-null float64
7 interest_rate_lock 10000 non-null bool
8 unit_cost_expansion 10000 non-null float64
9 value_of_time 10000 non-null float64
10 yield_curve 10000 non-null float64
11 free_flow_time 10000 non-null int64
12 initial_capacity 10000 non-null int64
13 no_build_travel_time 10000 non-null float64
14 build_travel_time 10000 non-null float64
15 time_savings 10000 non-null float64
16 value_of_time_savings 10000 non-null float64
17 cost_of_capacity_expansion 10000 non-null float64
18 present_cost_expansion 10000 non-null float64
dtypes: bool(1), category(1), float64(13), int64(4)
memory usage: 1.4 MB